掛け算の順序問題に決着はつくのか?「車が6台。1台に5人乗ると…」6×5か5×6か 文科省に聞いてみた

本文とは別の小学校に通う男児の掛け算の答案用紙。式を逆に書いて不正解となり、先生から「しきがぎゃくです」と赤字で指摘された
「1つ分の数×幾つ分」…1つ分とは?
現在小学3年の娘が2年だったとき、算数テストで「車が6台。1台に5人乗ると何人乗れるか」という設問があった。娘の書いた式は「6×5」だった。「6台の車に1人ずつ乗せていくから6人で、それを5回繰り返す」と考えたからだが、バツが付けられた。
文科省の「小学校学習指導要領解説 算数編」によれば、小2で掛け算を教える際、「1つ分の数×幾つ分」の順で式を立てることになっている。例えば「4人にみかんを3個ずつ配ると何個?」の答えを求める場合、「1つ分=3個」×「幾つ分=4人」となり、順序は「3×4」となる。
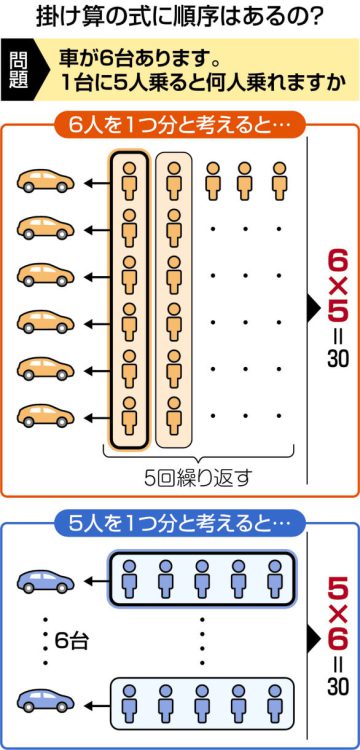
娘の先生も「1台あたり5人」を1つ分の数ととらえて「5×6」だけを正解としたのだ。
70年代から論争 教員にも苦手意識
「掛け算順序論争」は、1972年の朝日新聞の記事が発端だった。逆順の式をバツとされた小学生の保護者が文部省(当時)などに訴えた。「問題の意味を理解しているのか判断できる」と主張する順序肯定派に対し、否定派は「型通りの指導は考える力を阻害する」などと反論。数学者まで巻き込んで論争が繰り返されてきた。
「順序が逆だと△にする先生が多い気がする。×にするのをおびえているところはあるかも」と打ち明けるのはある小学校教諭だ。「私の感覚では、周りの先生の半数以上は『小2の掛け算の○付けは嫌だよね』という意識を持っている」と続けた。
アンケートでは83%が「どちらでも」
一方、別の小学校教員は「(逆順をバツにするなど)機械的に採点する先生もいる。保護者とトラブルになるのは説明不足もあると思う」と強調する。この教員は、保護者会で親にも掛け算の解釈やテストの扱いを説明しているという。
大手予備校「河合塾」講師の迫田昂輝(さこだこうき)さんが2年前、小学校の教員や塾講師ら100人にSNSでアンケートしたところ、83%が「順番はどちらでもよい」と回答した。迫田さんは「順番にこだわるのは一部の教員だけではないか」とみる。
「文科省も順序論争を意識している」
2020年度から使用されている指導要領解説では、掛け算に関する記述を増やし、「逆順」についても例示した。
「かけ算には順序があるのか」の著書もある算数史家の高橋誠さんは、掛け算の記述が増えたことに「文科省も順序論争を意識している」と見て取る。
結局どうなの?「先生の判断による」
しかし、文科省はあくまでも従来の順序が「自然である」としている。担当者に尋ねると、「式の順序を変えるなど計算の工夫はいろいろあっていいが、基本的に式には順序がある。そこはちゃんと教えましょうねということを解説で書いている」。では結局のところ、式を逆に書いたら○なの?×なの? 文科省の見解は「先生の判断によると思います」だった。
女性は問いかける。「何を一つ分と考えるかは、見方次第で変わる。一つの考え方を押しつける指導は、多様性を重んじる今の時代に逆行していませんか」
◇この記事に寄せられた感想や意見をまとめました。
「算数の掛け算の順序」を取り上げた記事に反響 「納得できない理由で×にされ、ショック」の声も より広い議論を(7月7日)
なるほど!
グッときた
もやもや...
もっと
知りたい










順序固定派の言う事が全く分からないのは、教師自身は交換法則が成り立つことを知っており、高学年になればそれを習う事をも知っているうえで、交換法則を適用した式は間違いであると主張する点だ。
「まだ習っていないから」というのならば、足し算の勉強を始める前に1+1=2の証明をしたのだろうか? もちろんそんなことはなく、「自明である」で片づけたはずだ。習っていなくても正しいものは正しいのだから。
オレンジの図
6台の車に1人ずつ乗る(6)
同じ台数に5人ずつ乗るので上記の5倍で
6✕5
青の図
1台の車に5人ずつ乗る(5)
6台の車に同じ人数ずつ乗るので上記の
6倍で 5✕6
何方も
6台の車に5人ずつ乗る時の総人数を
表す式です。
≪…「1つ分の数×幾つ分」の順で式を立てる…≫を、正六角形が正三角形(△)六つで構成されるコトで観る。
≪…「車が6台。1台に5人乗ると何人乗れるか」…≫は、[1台]を[△]とし、[車6台]が[△]6個と観ると、
5(人/台)× 6(台)=30(人)
これを、△で観ると、
5(△ 5人/1個)× 6(△ 6個/5人)=30(n)
[カタチ]先で、△(車)を[人]に置き換えると、[5](n 人)
置き換えた[△]の[5人]に、[△]の6倍と式(「1つ分の数×幾つ分」)を観る。
数(ヒフミヨ・自然数)の計算が、掛け算( 1×1 平方(□) )で計算できているのを、
正三角形(△)と凧型(△二つ)と台形(△三つ)で、六角形(△六つ)になっている。
この数式は、
掛け算(1×1 平方(□))の[カタチ]で纏め上げているのは、
数(n)の世界を平方(□)で観る数え上げの式、
(1/6)(2n+1)(n+1)n
この数式の意味(方程式の0の意味)は、
正六角形を掛け算(1×1)の世界を、台形と凧型と正三角形とで纏め上げたモノの全体の[1]は、△が、掛け算(1×1)の世界を、部分(△)と全体(△六つ)で纏め上げている。
このナラティブは、絵本の力で・・・
もろはのつるぎ(有田川町電子図書館)
掛け算の順序は、[ヒト]の成長と共に[こころ]に呑み込まれていく・・・
解釈図の上のところに「回」という単位が出てきたが文章には出てきていないので不適切
そもそも1単位の単価として出すものの単位は最終的な解答と同一である必要があるので車の台数を単価として取扱うのは不適切である
図上では人として描かれているが全ての車に1人は乗るという計算ならばそれは台数である
乗算の定義から見直そう
(6台の車に)1人ずつ乗車
✕5人ずつ乗車=6✕5=30人
逆にしても成立する。
6台に一人ずつ、1台につき5人になるまで座っていくとかんがえれば
6台✕1人/台+6台✕1人/台
+6台✕1人/台+6台✕1人/台
+6台✕1人/台=30人 とも考えられる。
何方でもありだと思います。
導入は順番通りに教えても、式を逆に書いても○でよいのでは。逆にするとウサギの耳が3本になるとか、答えの単位が違うからとか、そちらの説明の方が混乱を示すと思う。
また、順番通りに答えようとしても算数が苦手になるかもしれないし、逆に九九はもとより交換法則やトランプ配りの法則が分かる児童もいるかもしれないので、多様化された御時世の中で拘る必要はないと考えます。
この問題は、昔から目にする。どちらの結論にも、もっともらしい反論が可能なので、完全決着は、今後とも難しいように思う。
自分は、「どちらでも○」派であり、そのひとつの理由は、「掛け算」は、順序を入れ替えても、結果が変わらない、ということを、積極的に知る(そして使う)方がよい、と考えるからだ。
項の順序を入れ替えても、演算などの結果が変わらないという性質は、交換則が成り立つと表現し、四則演算では、加算でも成り立ち、減算と除算では成り立たない。
掛け算でも、項同士が行列や、行列式になると、交換則は成り立たなくなる。
このように、当たり前のようにも思える交換則が、成り立たない場合もあるということを、頭の片隅に入れて置くことは、四則演算を、少し「引いて見る」ことになり、そのような見方は、算数から、抽象性の高い数学に進む過程で、資するところがあると思う。
掛け算の順序を入れ替えた式を✕(バツ)にすると、その計算式を立てた状況に、当事者(回答者と判定者)を縛り付ける議論となり、掛け算という演算の性質を見通す広い視点の獲得を阻害する効果を持ってしまうのではないか。
このような観点から、私としては、掛け算の順序を入れ替えても、○としたい。
双方の考えに理があるように思われるので、どちらでも良いのではないか。因みに私は「5人一つ分」説でものを考えている。子供の主張に理屈が通っているのなら×を○にしてあげても良いのではないか。
元教員だけど、順序もしっかり見るとやる気を損なわせると言われ、順序が違っても丸にするときちんと採点してくださいと言われる。結局全ての人を納得させるなんて無理でしょ
結局文科省はお役所仕事で、今までそれでよかったならこれからもそれで良いと考えている。
メールのPPAP問題と根底は同じではないか。
本来、子どものための教育のはずが、それをなしていない。
なんで数学の問題に国語の理解ができてるかを二重で採点しているのか。順序が大事って言い張るのは文系脳だと思います。答えを出すために計算式を作ることができれば問題ない。
問題に、括り方とか指定があるんだったら、順番通りにやらなきゃいけないと思うけど、指定がないんだったら、◯でいいと思う。少なくとも、✕ではなく△でいいと思う。
車の問題はどっちでもいいと思うが、画像に出ているテストは一問目に一つ分の数✕いくつ分とあるので、順番が必要と思う。
2問目のシュークリームが一つ分=5個とは流石に見れない。
掛け算の順番というより、問題文に合わせて答えられなかったので不正解という認識でいいのでは?
小さい順に答えよで3,2,1ならだめですよね?
文章を式にして理解を深めるという練習なので、考えかたはこの場合人数×台数が正解。どっちでも良いことは無い。式が逆なのは理解不足なので丸では無い。
逆に算数以外の問題(資格試験など)で、これが理解出来てない人が問題を作るとどっちを答えるか分からない文章を作る。算数だから、ではなく学問は全て繋がっているのだから、この例は勉強不足。
暗記すればいいのではなく、物の成り立ちを考えて理解する習慣を身につけて欲しい。これで丸ついたら、その子は考えなくなるでしょう。
順序は本質ではなく、乗算の式に物理的モデルを見出す派閥と抽象化する派閥の対立に帰着する問題だ。
前者ならキュウリが3本入った袋が4つあるときの状況は3[本/袋] * 4 [袋] = 12 [本] という次元量の話になる。自称「順序」派も次元を書き添えてもらえれば、どちらが先に書かれていようが誰も異を唱えるまい。(であるのに[本/袋]を[本]として誤魔化しつつ、この誤魔化しを順序を固定することによって糊塗している時点で順序派はおかしなことをやっているのだが)。
他方、非順序派はキュウリが袋に3本ずつ4袋だろうが、4本ずつ3袋だろうがそれを
****
****
****
という次元の区別のない理解へと抽象化することを求めている。そして、数年後には学ばざるを得ない数学の前段階として身につけるべきはこちらの抽象化なのだ。
合計何人と答えを出す場合、掛算の最初は人の数が来ると中学校の先生に40数年前に習いました。その教えが正しいのなら、5人×6台=30人の順番です。
乗法(かけ算)の交換法則(5×6=6×5)とか、中学校いったら習うけど、子どもが、なぜその考え(式)にたどり着いたかが、説明できるのが1番大事。結局のところ文科省の官僚様は現場の指導をわからない人も多いし、融通の聞かない子どもに考えさせずに押し付けて洗脳する現場の教員も問題。
この場合、問題文に指定があるのでその通りに書いたほうが良いと思います。逆におまけで正解にしてしまうと子供が多少、文章を見落としても『結局、正解になるんだ』と思いがちになると思います。
小3以上の問題でかけ算の順番の指定がある問題は、ほぼないと思います。交換法則(a×b=b×a)が成り立ちますので計算結果が合っていれば正解にせざるをえません。
しかし、問題文に指定がある場合は、読み取って書けたほうがいいと思います。(個人的にはどっちでもええけどなw)
>2023/07/08 17:26
それでは車が6台というグループが存在しないので間違いなのは明らかです
順番にこだわる方に、「4x100mリレー」について順番をどのように理解するのか聞いてみたいです。
え?分からないの?勉強が出来ない少数派の意見をいちいち取り上げなくてもいいよ。
これを単に算数だけの問題として捉えているのがいけない。問題文をしっかり読み解けているのかというのが大切。
この場合は『1台に5人乗る』と問題で決められているのだから、1台につき5人のグループとなる。それが6台分なので
1×5+1×5+1×5+1×5+1×5+1×5
= 5×6 となる。
これを逆にするなら
6×5
=1×6+1×6+1×6+1×6+1×6
となるのだが、この式では『1台に5人』というグループが存在しないことになる。
結果は同じでも問題の要件を満たしていないので間違いとなるのではないでしょうか。
問題の解き方の順番も理解してもらいたい意図は分かるが、結果は合っているのだからどちらも正解にして、子供たちに何でその順番で計算したか理由を聞いてあげるのが良いのでは。
確かにこの論争は前から叫ばれているイメージがありました。
私の時は逆式はバツでしたが,挿絵の考え方にするとマルになるのでどちらでもいいと思います。